Hairpin vortices and other turbulent phenomena

Living and dying within the turbulent boundary layers and wakes of every Formula 1 car, is a taxonomical cornucopia of transient hydrodynamical beasties. The ecology of these lifeforms is determined by the exact geometry and Reynolds number of the flow regime in question, but it is still possible to identify some general phenomena.

First recall that turbulence can be defined as the existence of chaotic vorticity over a range of different length and time scales, the vorticity on larger length scales cascading down to smaller length scales, where it is dissipated as heat. Now, vorticity can be packaged in the form of sheets and tubes, and these structures are subject to the following two general processes, (see Turbulence, P.A.Davidson, CUP 2004, pp206-210):

(i) Vortex tubes tend to stretch, and upon stretching, they 'burst' into vortex sheets.

(ii) Vortex sheets rolls up under Kelvin-Helmholtz instability into sequences of vortex tubes, (as seen in the diagram just above here).

As a result of these processes, the vorticity in a fluid is extruded into increasingly thinner sheets and tubes, until eventually it reaches the length scales at which viscous effects dominate, and the turbulent energy is dissipated into heat.

In a turbulent boundary layer, however, are special types of coherent structures dubbed hairpin vortices.


P.A.Davidson's explanation for the generation of these hydrodynamical parasites, (ibid., p141-142), begins by assuming the existence of spanwise vortex lines in the boundary layer. A turbulent streamwise fluctuation in the velocity field distorts such vortex lines, creating perturbed segments which resemble sections of a vortex ring. Vorticity generates its own velocity field, and the curvature in the perturbed vortex tube causes the tip of the tube to rise upwards. The higher the tip of the vortex rises in the boundary layer, the higher the mean streamwise velocity, with the consequence that the vortex tube gets stretched even further in a streamwise direction. This is a positive feedback process, causing the tip of the vortex to rise yet higher.

Elsewhere, in those parts of the turbulent wakes which can be idealised as regions of isotropic turbulence, the smallest vortices (so-called 'worms') can be idealised as Burgers vortices. A Burgers vortex is an exact solution of the Navier-Stokes equations, in which the vorticity has a constant Gaussian distribution around a particular axis. The constancy arises because the outward diffusion of vorticity perpendicular to the axis, is exactly balanced by the stretching of the fluid flow parallel to the axis.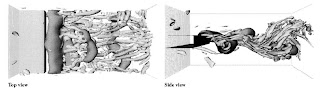

Over the coming decades, complete solutions of the Navier-Stokes equations, so-called Direct Numerical Simulations (DNS), will steadily unveil these complex ecologies. To gain a feel for this hidden complexity, take a look at the DNS study conducted by Sandham et al (2001) of a trailing edge flow at a Reynolds number of ~ 1000.

Now, at this Reynolds number, the wake turbulence contained a Karman vortex street; i.e, staggered rows of counter-rotating spanwise vortices. What Sandham et al found was that the spanwise Karman vortex street interacts in a complex manner with the streamwise vortex tubes generated in the turbulent boundary layer upstream of the trailing edge. In fact, the streamwise vortex tubes strain, intensify, and eventually destroy the Karman vortices.

The flow regime of a Formula One car has a Reynolds number of ~ 10⁶, which is just about the upper limit for any sort of vortex street pattern to be distinguishable from random turbulence, so it's unlikely that this research is directly relevant to Formula 1. It is, however, an interesting taste of the hydrodynamical complexity yet to be revealed.